Fundamental Concepts Of Calculus: Types & Calculations

Last Updated: 25 March 2023

In mathematics, calculus is one of the main branches along with trigonometry, geometry, algebra, etc. It deals with the study of fundamental concepts of continuous change and motion. It is a frequently used technique in engineering, physics, economics, and even biology.

Calculus is the main topic of mathematics that deals with the slope of the tangent line and the area under the curve. In this article, we will explain the fundamental concept of calculus along with its definition, types, and solved examples.

Page Contents

What is Calculus?

Calculus is the fundamental branch of mathematics that is used to explain the study of the rate of change of functions and the addition of smaller quantities to find the larger quantities with the help of independent variables.

There are various sub-branches of calculus such as integration, differentiation, limit, continuity, power series, shell method, etc. All the sub-branches of calculus are the building block of mathematics that are used to evaluate various results easily and accurately.

Types of Calculus

There are two well-known types (AKA branches) of calculus:

Integral Calculus
Differential Calculus

Let’s describe both types of calculus briefly to understand their basics.

1. Integral Calculus

In mathematics, integral calculus is a sub-branch of calculus that deals with the study of the area under the curve. It is widely used to determine the numerical value and the new function whose original function is a differential function.

While the indefinite integral is the type of integration that is used to evaluate the new function whose original function is a differential function. The upper and lower limit values are not involved in this subtype of the integral.

The definite and indefinite integrals are frequently used to evaluate the area under the curve, the volume of the solid, and other related quantities. The general expression of the definite and indefinite integral is:

Indefinite Integral	Definite Integral
∫f(v) dv = F(v) + C	∫_a^b f(v) dv = [F(v)]^b_a = F(b) – F(a)
Where, 1) ∫ is the integral notation for indefinite integral. 2) f(v) is a differential function. 3) F(v) is the integral function. 4) v is the independent variable of the function. 5) C is the constant of integration.	Where, 1) ∫_a^b is the integral notation for definite integral. 2) a & b are the boundary values. 3) f(v) is a differential function. 4) F(v) is the integral function v is the independent variable of the function. 5) C is the constant of integration.

Rules of Integral Calculus

No.	Name Of The Rule	Rules	Examples
1	Power Rule	∫[f(v)]ⁿ dv = [f(v)ⁿ⁺¹ / n + 1] + C	Find the integral of v³ Solution: ∫[v³] dv = [v³⁺¹/3 + 1] + C ∫[v³] dv = [v⁴/4] + C
2	Sum Rule	∫[f(v) + g(v)] dv = ∫[f(v)] dv + ∫[g(v)] dv	Find the integral of v + v² Solution: ∫[v + v²] dv = ∫[v] dv + ∫ [v²] dv ∫[v + v²] dv = [v¹⁺¹/1 + 1] + [v²⁺¹ / 2 + 1] + C ∫[v + v²] dv = [v²/2] + [v³ / 3] + C
3	Difference Rule	∫[f(v) – g(v)] dv = ∫[f(v)] dv – ∫[g(v)] dv	Find the integral of v – v² Solution: ∫[v – v²] dv = ∫[v] dv – ∫ [v²] dv ∫[v – v²] dv = [v¹⁺¹/1 + 1] – [v²⁺¹ / 2 + 1] + C ∫[v – v²] dv = [v²/2] + [v³ / 3] – C
4	Constant Multiple Rule	∫[K * f(v)] dv = K * ∫[f(v)] dv	Find the integral of 4v⁵ Solution: ∫[4v⁵] dv = 4∫[v⁵] dv ∫[4v⁵] dv = 4∫[v⁵⁺¹ / 5 + 1] ∫[4v⁵] dv = 4∫[v⁶ /6] = 2v⁶/3

Examples of Integral Calculus

#Example 1: Indefinite Integral

Evaluate the integral of h(w) = 2w²– 4w³ + 6w⁵ with respect to w

Solution:

Step 1: First of all, take a differential function and apply the notation of integral to it.

h(w) = 2w²– 4w³ + 6w⁵

ʃ h(w) dw = ʃ [2w²– 4w³ + 6w⁵] dw

Step 2: Now use the above sum and difference rules.

ʃ [2w²– 4w³ + 6w⁵] dw = ʃ [2w²] dw– ʃ [4w³] dw + ʃ [6w⁵] dw

Step 3: Now apply the constant multiple rules.

ʃ [2w²– 4w³ + 6w⁵] dw = 2ʃ [w²] dw– 4ʃ [w³] dw + 6ʃ [w⁵] dw

Step 4: Integrate the above expression.

ʃ [2w²– 4w³ + 6w⁵] dw = 2 [w²⁺¹ / 2 + 1]– 4 [w³⁺¹ / 3 + 1] + 6 [w⁵⁺¹ / 5 + 1] + C

= 2 [w³ / 3]– 4 [w⁴ / 4] + 6 [w⁶ / 6] + C

= 2/3 [w³]– 4/4 [w⁴] + 6/6 [w⁶] + C

= 2/3 [w³]– [w⁴] + [w⁶] + C

#Example 2: Definite Integral

Evaluate the integral of f(u) = 5u⁴ + 6sin(u) – 10 with respect to u & the [1, 2] is the interval.

Solution:

Step 1: First of all, take the given differential function and apply the notation of integral to it.

ʃ^b_a [f(u)] du = ʃ²₁ [5u⁴ + 6sin(u) – 10] du

Step 2: Now use the above sum and difference rules.

ʃ²₁ [5u⁴ + 6sin(u) – 10] du = ʃ²₁ [5u⁴] du + ʃ²₁ [6sin(u)] – ʃ²₁ [10] du

Step 3: Now apply the constant multiple rules.

ʃ²₁ [5u⁴ + 6sin(u) – 10] du = 5ʃ²₁ [u⁴] du + 6ʃ²₁ [sin(u)] – ʃ²₁ [10] du

Step 4: Integrate the above expression.

ʃ²₁ [5u⁴ + 6sin(u) – 10] du = 5 [u⁴⁺¹ / 4 + 1]²₁ + 6 [-cos(u)]²₁ – [10u]²₁

ʃ²₁ [5u⁴ + 6sin(u) – 10] du = 5 [u⁵ / 5]²₁ + 6 [-cos(u)]²₁ – [10u]²₁

ʃ²₁ [5u⁴ + 6sin(u) – 10] du = 5/5 [u⁵]²₁ + 6 [-cos(u)]²₁ – 10 [u]²₁

ʃ²₁ [5u⁴ + 6sin(u) – 10] du = [u⁵]²₁ + 6 [-cos(u)]²₁ – 10 [u]²₁

Step 5: Apply the boundary values.

ʃ²₁ [5u⁴ + 6sin(u) – 10] du = [2⁵ – 1⁵] + 6 [-cos(2) + cos(1)] – 10 [2 – 1]

ʃ²₁ [5u⁴ + 6sin(u) – 10] du = [32 – 1] + 6 [-cos(2) + cos(1)] – 10 [2 – 1]

ʃ²₁ [5u⁴ + 6sin(u) – 10] du = 31 + 6 [-cos(2) + cos(1)] – 10 [1]

ʃ²₁ [5u⁴ + 6sin(u) – 10] du = 31 – 6cos(2) + 6cos(1) – 10

ʃ²₁ [5u⁴ + 6sin(u) – 10] du = 21 – 6cos(2) + 6cos(1)

You can take help from online antiderivative calculators to cross-check the results of integral problems.

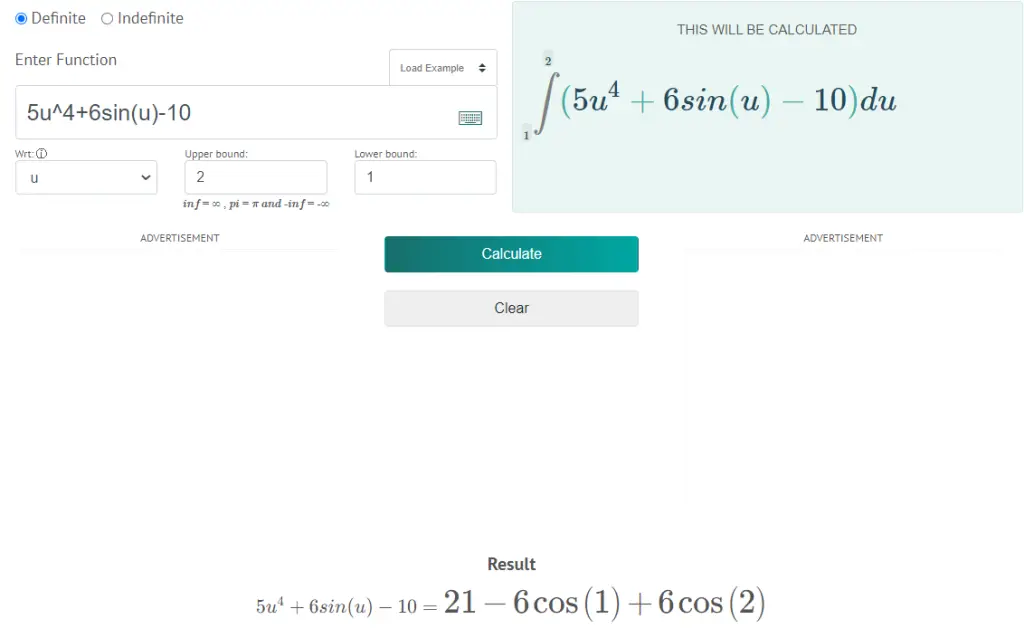
Image Source: https://www.antiderivativecalculator.net

2. Differential Calculus

In mathematics, differential calculus is one of the main branches of calculus that deals with the study of the rate of changes and slope of the curves (tangent lines). It calculates the changes in the given function when the input changes by a smaller amount.

The rate of change of the given function f(v) with respect to independent variable “v” is known as differential f’(v). The differential calculus is usually denoted by d/dv, f’(v), D[f(v)], etc. The process of finding the instantaneous rate of change of functions is known as differentiation.

The differential formula by the first principle is:

d/dv [f(v)] = lim_h→0 [f(v + h) – f(v)] / h

Rules of Differential Calculus

No.	Name Of The Rule	Rules	Examples
1	Power Rule	d/dv [f(v)]ⁿ = n [f(v)]^n-1 d/dv [f(v)]	Find the derivative of v⁴ Solution: d/dv [v⁴] = 4 [v^4-1] d/dv [v] d/dv [v⁴] = 4 [v³] (1) d/dv [v⁴] = 4v³
2	Constant Rule	d/dv [K] = 0	Find the derivative of 540 Solution: d/dv [540] = 0
3	Constant Multiple Rule	d/dv [K * f(v)] = K * d/dv [f(v)]	Find the derivative of 3v² Solution: d/dv [3v²] = 3d/dv[v²] d/dv [3v²] = 3 [2 v^2-1] d/dv [v] d/dv [3v²] = 3 [2 v¹] [1] d/dv [3v²] = 6v
4	Sum Rule	d/dv [f(v) + g(v)] = d/dv [f(v)] + d/dv [g(v)]	Find the derivative of 3v² + 4v³ Solution: d/dv [3v² + 4v³] = d/dv [3v²] + d/dv [4v³] d/dv [3v² + 4v³] = 3d/dv [v²] + 4d/dv [v³] d/dv [3v² + 4v³] = 3 [2 v^2-1] d/dv [v] + 4 [3 v^3-1] d/dv [v] d/dv [3v² + 4v³] = 3 [2 v] + 4 [3 v²] d/dv [3v² + 4v³] = 6v + 12v²
5	Difference Rule	d/dv [f(v) – g(v)] = d/dv [f(v)] – d/dv [g(v)]	Find the derivative of 2v² – 6v³ Solution: d/dv [2v² – 6v³] = d/dv [2v²] – d/dv [6v³] d/dv [2v² – 6v³] = 2d/dv [v²] – 6d/dv [v³] d/dv [2v² – 6v³] = 2 [2 v^2-1] d/dv [v] – 6 [3 v^3-1] d/dv [v] d/dv [2v² – 6v³] = 2 [2 v] – 6 [3 v²] d/dv [2v² – 6v³] = 4v – 18v²

The problems of differentiation can be solved with the help of a differential calculator according to the above rules.

Example of Differential Calculus

#Example

Find the differential of p(w) = 2w³ + 12w⁴ + 16w – 12u⁵ + 2cos(w) – 3w⁶ + 12 with respect to “w”.

Solution:

Step 1: First of all, take the given expression and apply the notation of differentiation to it.

p(w) = 2w³ + 12w⁴ + 16w – 12u⁵ + 2cos(w) – 3w⁶ + 12

d/dw [p(w)] = d/dw [2w³ + 12w⁴ + 16w – 12u⁵ + 2cos(w) – 3w⁶ + 12]

Step 2: Use the above sum and difference laws of differential calculus.

d/dw [2w³ + 12w⁴ + 16w – 12u⁵ + 2cos(w) – 3w⁶ + 12] = d/dw [2w³] + d/dw [12w⁴] + d/dw [16w] – d/dw [12u⁵] + d/dw [2cos(w)] – d/dw [3w⁶] + d/dw [12]

Step 3: Now use constant multiple rules of differential calculus.

d/dw [2w³ + 12w⁴ + 16w – 12u⁵ + 2cos(w) – 3w⁶ + 12] = 2d/dw [w³] + 12d/dw [w⁴] + 16d/dw [w] – 12u⁵ d/dw [1] + 2d/dw [cos(w)] – 3d/dw [w⁶] + d/dw [12]

Step 4: Now the power and constant rules of differential calculus.

d/dw [2w³ + 12w⁴ + 16w – 12u⁵ + 2cos(w) – 3w⁶ + 12] = 2 [3 w^3-1] + 12 [4 w^4-1] + 16 [w^1-1] – 12u⁵ [0] + 2 [-sin(w)] – 3 [6 w^6-1] + [0]

d/dw [2w³ + 12w⁴ + 16w – 12u⁵ + 2cos(w) – 3w⁶ + 12] = 2 [3 w²] + 12 [4 w³] + 16 [w⁰] – [0] + 2 [-sin(w)] – 3 [6 w⁵] + [0]

d/dw [2w³ + 12w⁴ + 16w – 12u⁵ + 2cos(w) – 3w⁶ + 12] = 2 [3 w²] + 12 [4 w³] + 16 [1] + 2 [-sin(w)] – 3 [6 w⁵]

d/dw [2w³ + 12w⁴ + 16w – 12u⁵ + 2cos(w) – 3w⁶ + 12] = 6w²] + 48w³ + 16 – 2sin(w) – 18w⁵

Conclusion

Calculus is a fundamental branch of mathematics that deals with various quantities such as the area under the curve and the slope of the tangent line. There are further many branches of calculus but integral calculus and differential calculus are two main kinds of calculus.

Integral calculus is the study of the area under the curve and evaluating the numerical value and new function with respect to integrating variables. While differential calculus is the instantaneous rate of change of a function with respect to a variable.

Read More